1 TABLE OF CONTENTS

1 TABLE OF CONTENTS..................................................................................................................................................... 1

2 INTRODUCTION................................................................................................................................................................. 2

3 "HURRYORDER": A NEW APPROACH....................................................................................................................... 3

3.1 Sorting with a SORTING Algorithm................................................................................................................. 3

3.2 Ordering with an ORDERING Algorithm........................................................................................................ 3

4 THE EVALUATION OF ORDERING ALGORITHMS.................................................................................................. 4

5 THE TWO VERSIONS OF "HURRYORDER".............................................................................................................. 4

6 A COMPARISON OF "HURRYORDER" WITH CONVENTIONAL ALGORITHMS.......................................... 5

6.1 What Is Shown by the Test Results................................................................................................................ 7

6.2 Evaluation..................................................................................................................................................................... 7

7 A SHORT SUMMARY CONCERNING "HURRYORDER"........................................................................................ 9

7.1 Areas Where "Hurryorder" Can Be Used...................................................................................................... 9

7.2 Strengths of "Hurryorder"................................................................................................................................. 9

7.3 Weaknesses of "Hurryorder"............................................................................................................................. 9

8 APPENDICES I AND II: A COMPARISON OF ORDERING AND SORTING ALGORITHMS....................... 10

2 INTRODUCTION

In the field of computer science there is hardly an area which has been so thoroughly analyzed as the one dealing with the sorting and determination of information in data banks.

The rapid development of hardware makes possible the construction of increasingly fast computers. But ultimately it is the software which determines how efficiently a computer functions. A good algorithm installed on a slow computer often performs better than a fast computer with a poor algorithm.

When dealing with large volumes of data, the capability of sorting, ordering or evaluating the data in accordance with optional criteria and within the shortest time possible is of crucial importance. Therefore, ordering and searching in data banks continues to play a central role in computer science.

In this short paper I wish to introduce you to my newly developed ordering algorithm called "Hurryorder."

The advantages of "Hurryorder" can be summarized as follows:

• fast, high-performance and thus economical processing (sorting, arrangment, evaluation) of large amounts of data (at ten times the speed of conventional algorithms!),

• flexible configuration of the ordering key,

• stable sorting.

What "Hurryorder" is and where its incomparable efficiency lies is described in the following.

3 "HURRYORDER": A NEW APPROACH

"Hurryorder" is an algorithm by means of which data can be ordered. Although the word "SORT" occurs in the name of most ordering and sorting algorithms,¹ in naming "Hurryorder," the word "ORDER" was deliberately included.

At this point a brief explanation of the difference between a SORTING and an ORDERING algorithm is appropriate:

3.1 Sorting with a SORTING Algorithm

"Sorting" is generally conceived of as the process of arranging a quantity of given items in an ascending or descending order in terms of the respective values of the items.

3.2 Ordering with an ORDERING Algorithm

"Ordering" is conceived of as the process of arranging a quantity of items in an <<optional>> order with respect to the values of the items. Understood in this way, a sorting algorithm comprises a part of an ordering algorithm.

The procedure can, generally speaking, be broken down into two categories. The first category includes the arranging of arrays, which can be optionally accessed, the other the arranging of sequential data. "Hurryorder" belongs to the first category. "Hurryorder" orders items in arrays by means of optional access (e.g., in RAM and on hard disks and floppy disks).

With "Hurryorder" the arrangement of data in ascending or descending order, as performed by conventional ordering and sorting algorithms, is not compulsory. How the data is arranged can be chosen with great flexibility, yet without a reduction of efficiency.

______________________

[1] Because both ordering and sorting are constituent parts of the new method, the more comprehensive term "ordering and sorting algorithm" is used in this paper, even though ordering is not a part of the older methods.

4 THE EVALUATION OF ORDERING ALGORITHMS

The two most important criteria for the evaluation of an ordering and sorting algorithm are reflected in the questions:

• How quickly can the algorithm arrange data?

• Is the algorithm stable or non-stable?

The speed of an ordering and sorting algorithm is without question of utmost significance.

5 THE TWO VERSIONS OF "HURRYORDER"

There are two versions of "Hurryorder." The difference between the two versions lies in the fact that one is stable, the other not.

The non-stable version of Hurryorder is called "Hurryorder n.s." The stable version of Hurryorder is called "Hurryorder s."

Since both versions function in essentially the same way, their performance curves are almost identical.

Although there are no real disadvantages in a stable algorithm vis-à-vis a non-stable one, two versions were created for this reason: The stable algorithm ("Hurryorder s") requires more temporary memory for each item to be sorted. That can be a problem if there is not enough random access memory available. Therefore, the non-stable algorithm "Hurryorder n.s." is more suitable in cases where the stable sorting of data is not necessary and little memory is available.

Among the commonly used ordering and sorting algorithms tested, the program "Quicksort" delivers the best results by a wide margin.

The sorting algorithm "Quicksort" is generally regarded as the best sorting algorithm currently available.

It should be mentioned that "Quicksort" cannot perform stable sorting.

6 A COMPARISON OF "HURRYORDER" WITH CONVENTIONAL ALGORITHMS

Computer Used in the Test:

Computer 80486 DX2 66Mhz. (internal cache enabled).

Programs Tested:

HURRYNS1	EXE	"Hurryorder" non-stable	16-Bit Comp
32HUNS1	EXE	"Hurryorder" ident. with HURRYNS1 except	32-Bit Comp
HURRYNS2	EXE	"Hurryorder" non-stable (address far)	16-Bit Comp
HURRYS1	EXE	"Hurryorder" stable	16-Bit Comp
32HUS1	EXE	"Hurryorder" ident. with HURRYS1 except	32-Bit Comp
HURRYS2	EXE	"Hurryorder" stable (address far)	16-Bit Comp
QUICK1	EXE	Quicksort	16-Bit Comp
32QUICK1	EXE	Quicksort ident. with QUICK1 except	32-Bit Comp
QUICK2	EXE	Quicksort (address far)	16-Bit Comp
BUBBLE1	EXE	Bubblesort	16-Bit Comp
HEAP1	EXE	Heapsort	16-Bit Comp
SHELL1	EXE	Shellsort	16-Bit Comp
EXCHANG1	EXE	Exchangesort	16-Bit Comp
INSERT1	EXE	Insertsort	16-Bit Comp

The following important points supplement the information provided by the table:

• All the algorithms are implemented in the programming language "C."

• All the programs listed perform the same task.

• The programs sort the values of integers.

• The range of these values lies between -2147483647 and +2147483647.

• The data bank with the items to be sorted (integer values) is located on a hard disk. The data bank is not altered by the sorting process. What is sorted are indices. The size of the index required by each record is 4 bytes. The indices are managed in RAM.

• Two bytes of temporary memory are required for each record when using Hurryns1.exe and Hurryns2.exe (memory is released upon completion of the sorting process).

• Six bytes of temporary memory are required for each record when using Hurrys1.exe and Hurrys2.exe (memory is released upon completion of the sorting process).

6.1 What Is Shown by the Test Results

• The number of times that the data bank is accessed.

• The number of times that objects are exchanged during the procedure.

• The time required for sorting (in seconds).

6.2 Evaluation

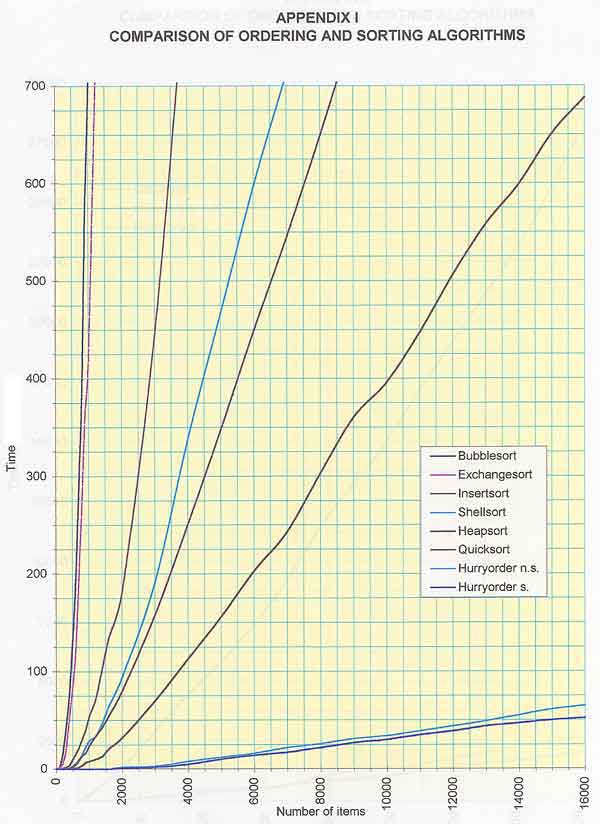
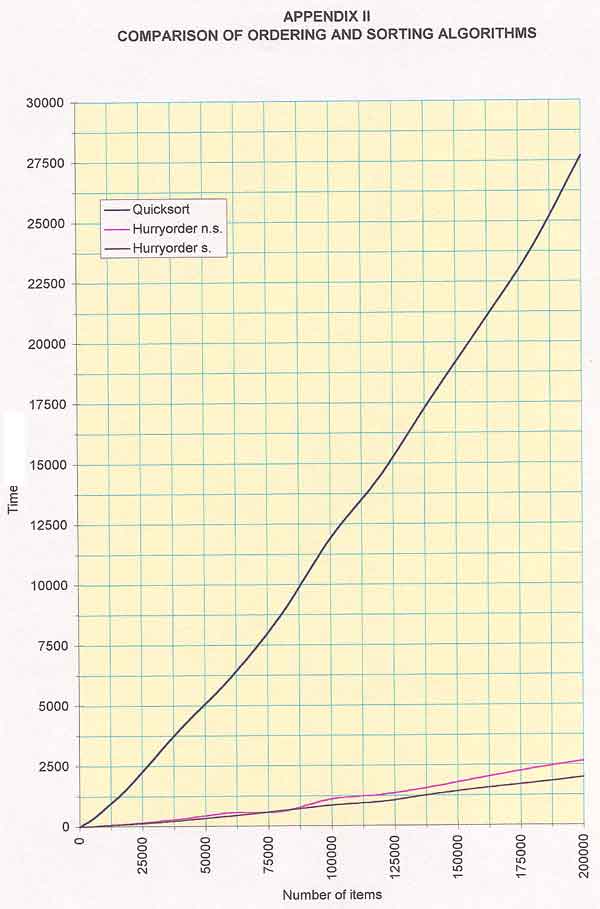
The test results demonstrate the unparalleled efficiency of "Hurryorder." Of all the conventional ordering and sorting algorithms, "Quicksort" exhibits — as expected — the best results.

Performing under the same conditions, "Hurryorder" functions many times more efficiently than "Quicksort." Furthermore, one "Hurryorder" version can sort stably, something of which "Quicksort" is incapable.

In order to arrange the data, "Hurryorder" must access it only a limited number of times, and requires a comparatively small number of exchange operations.

The diagrams in the Appendix "A Comparison of Ordering and Sorting Algorithms" illustrate the unmatched efficiency of "Hurryorder."

The data bank is comprised of uniformly distributed random numbers. Range of the values:

-2147483640 to +2147483640.

ALGORITHM

ITEMS

NO. OF

TIMES

ACCESSED

NO. OF

ITEM

EXCHANGES

SORTING

TIME

CHECK

PRO-GRAM

BUBBLESORT n.s.

EXCHANGESORT

INSERTSORT

SHELLSORT

HEAPSORT

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

1600

2557140

1290043

676793

63226

51567

24319

3245

638515

1593

674448

18015

18197

4372

2553

3245

2175.0

1271.0

135.0

65.0

50.0

21.0

1.0

bubble1

exchang1

insert1

shell1

heap1

quick1

hurryns1

hurrys1

INSERTSORT

SHELLSORT

HEAPSORT

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

5000

6488128

226204

185172

86933

10364

6480685

60728

64780

15599

9126

10364

1300.0

467.0

348.0

156.0

12.0

10.0

quick2

hurryns2

hurrys1

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

10000

182280

21402

33833

19147

21402

396.0

34.0

27.0

quick2

hurryns2

hurrys2

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

16000

305000

35460

56600

31494

35460

688.0

65.0

50.0

quick2

hurryns2

hurrys2

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

40000

908418

98386

149844

83290

98386

4021.0

313.0

237.0

32quick1

32huns1

32hus1

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

80000

1848276

217636

322076

176217

217636

8697.0

605.0

630.0

32quick1

32huns1

32hus1

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

120000

2948401

360309

502142

244791

360309

14483.0

1193.0

559.0

32quick1

32huns1

32hus1

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

160000

3860624

471762

684902

377852

471762

20691.0

1977.0

1537.0

32quick1

32huns1

32hus1

QUICKSORT

HURRYORDER n.s.

HURRYORDER s.

200000

5151688

599532

863227

483586

599532

27695.0

2652.0

1967.0

32quick1

32huns1

32hus1

7 A SHORT SUMMARY CONCERNING "HURRYORDER"

The test results plainly show that the algorithm "Hurryorder" orders data very efficiently. No other ordering and sorting algorithm known is able to order and sort information stored on RAM disks, floppy disks, hard disks, etc. with anywhere near the speed of "Hurryorder."

As already mentioned, one of the greatest strengths of "Hurryorder" is that it can not only sort but also order data. Its ordering efficiency is comparable with its sorting efficiency. Sorting, as performed by the programs tested, is just one specific variant of ordering.

7.1 Areas Where "Hurryorder" Can Be Used

"Hurryorder" can be employed in a large number of areas. It makes sense to use "Hurryorder" wherever large quantities of data need to be sorted, ordered or evaluated in accordance with a wide variety of criteria.

7.2 Strengths of "Hurryorder"

• Unparalleled efficiency when ordering data stored on peripheral data carriers (hard disks, floppy disks, optical disks, etc.) by means of optional access. On the average, the ordering of data is accomplished ten times faster than by "Quicksort."

• The capacity to order data.

• How the data is arranged can be configured with great flexibility.

• One version of "Hurryorder" can perform stable sorting.

• The data bank is accessed a minimal number of times.

7.3 Weaknesses of "Hurryorder"

• Moderate efficiency where there are few items to order (number < 100).

• "Hurryorder stable" requires six bytes of temporary memory per item.

• "Hurryorder non-stable" requires two bytes of temporary memory per item.

APPENDICES I AND II:

A COMPARISON OF

ORDERING AND SORTING ALGORITHMS

Back

Print this page